Filters
Question type
Study Flashcards

Identify the equation without completing the square. - 2y2−2x−3y=02 y ^ { 2 } - 2 x - 3 y = 0


A) hyperbola
B) ellipse
C) parabola
D) not a conic

Correct Answer

verifed

verified

Discuss the equation and graph it. - r=42−sin⁡θr = \frac { 4 } { 2 - \sin \theta }


A) directrix perpendicular to polar axis 8 right of pole
center (−815,0) \left(-\frac{8}{15}, 0\right)
vertices (83,π) ,(85,0) \left(\frac{8}{3}, \pi\right) ,\left(\frac{8}{5}, 0\right)
Discuss the equation and graph it. - r = \frac { 4 } { 2 - \sin \theta } A) directrix perpendicular to polar axis 8 right of pole center \left(-\frac{8}{15}, 0\right) vertices \left(\frac{8}{3}, \pi\right) ,\left(\frac{8}{5}, 0\right) B) directrix parallel to polar axis 8 above pole center \left(-\frac{8}{15}, \frac{\pi}{2}\right) vertices \left(-\frac{8}{5}, \frac{3 \pi}{2}\right) ,\left(\frac{8}{3}, \frac{3 \pi}{2}\right) C) directrix perpendicular to polar axis 8 left of pole center \left(\frac{8}{15}, 0\right) vertices \left(\frac{8}{5}, \pi\right) ,\left(\frac{8}{3}, 0\right) D) directrix parallel to polar axis 8 below pole center \left(\frac{8}{15}, \frac{\pi}{2}\right) vertices \left(\frac{8}{3}, \frac{\pi}{2}\right) ,\left(\frac{8}{5}, \frac{3 \pi}{2}\right)

B) directrix parallel to polar axis 8 above pole center (−815,π2) \left(-\frac{8}{15}, \frac{\pi}{2}\right) vertices (−85,3π2) ,(83,3π2) \left(-\frac{8}{5}, \frac{3 \pi}{2}\right) ,\left(\frac{8}{3}, \frac{3 \pi}{2}\right)

Discuss the equation and graph it. - r = \frac { 4 } { 2 - \sin \theta } A) directrix perpendicular to polar axis 8 right of pole center \left(-\frac{8}{15}, 0\right) vertices \left(\frac{8}{3}, \pi\right) ,\left(\frac{8}{5}, 0\right) B) directrix parallel to polar axis 8 above pole center \left(-\frac{8}{15}, \frac{\pi}{2}\right) vertices \left(-\frac{8}{5}, \frac{3 \pi}{2}\right) ,\left(\frac{8}{3}, \frac{3 \pi}{2}\right) C) directrix perpendicular to polar axis 8 left of pole center \left(\frac{8}{15}, 0\right) vertices \left(\frac{8}{5}, \pi\right) ,\left(\frac{8}{3}, 0\right) D) directrix parallel to polar axis 8 below pole center \left(\frac{8}{15}, \frac{\pi}{2}\right) vertices \left(\frac{8}{3}, \frac{\pi}{2}\right) ,\left(\frac{8}{5}, \frac{3 \pi}{2}\right)

C) directrix perpendicular to polar axis 8 left of pole
center (815,0) \left(\frac{8}{15}, 0\right)
vertices (85,π) ,(83,0) \left(\frac{8}{5}, \pi\right) ,\left(\frac{8}{3}, 0\right)
Discuss the equation and graph it. - r = \frac { 4 } { 2 - \sin \theta } A) directrix perpendicular to polar axis 8 right of pole center \left(-\frac{8}{15}, 0\right) vertices \left(\frac{8}{3}, \pi\right) ,\left(\frac{8}{5}, 0\right) B) directrix parallel to polar axis 8 above pole center \left(-\frac{8}{15}, \frac{\pi}{2}\right) vertices \left(-\frac{8}{5}, \frac{3 \pi}{2}\right) ,\left(\frac{8}{3}, \frac{3 \pi}{2}\right) C) directrix perpendicular to polar axis 8 left of pole center \left(\frac{8}{15}, 0\right) vertices \left(\frac{8}{5}, \pi\right) ,\left(\frac{8}{3}, 0\right) D) directrix parallel to polar axis 8 below pole center \left(\frac{8}{15}, \frac{\pi}{2}\right) vertices \left(\frac{8}{3}, \frac{\pi}{2}\right) ,\left(\frac{8}{5}, \frac{3 \pi}{2}\right)

D) directrix parallel to polar axis 8 below pole center (815,π2) \left(\frac{8}{15}, \frac{\pi}{2}\right) vertices (83,π2) ,(85,3π2) \left(\frac{8}{3}, \frac{\pi}{2}\right) ,\left(\frac{8}{5}, \frac{3 \pi}{2}\right)
Discuss the equation and graph it. - r = \frac { 4 } { 2 - \sin \theta } A) directrix perpendicular to polar axis 8 right of pole center \left(-\frac{8}{15}, 0\right) vertices \left(\frac{8}{3}, \pi\right) ,\left(\frac{8}{5}, 0\right) B) directrix parallel to polar axis 8 above pole center \left(-\frac{8}{15}, \frac{\pi}{2}\right) vertices \left(-\frac{8}{5}, \frac{3 \pi}{2}\right) ,\left(\frac{8}{3}, \frac{3 \pi}{2}\right) C) directrix perpendicular to polar axis 8 left of pole center \left(\frac{8}{15}, 0\right) vertices \left(\frac{8}{5}, \pi\right) ,\left(\frac{8}{3}, 0\right) D) directrix parallel to polar axis 8 below pole center \left(\frac{8}{15}, \frac{\pi}{2}\right) vertices \left(\frac{8}{3}, \frac{\pi}{2}\right) ,\left(\frac{8}{5}, \frac{3 \pi}{2}\right)

Correct Answer

verifed

verified

Rotate the axes so that the new equation contains no xy-term. Discuss the new equati - 17x2−12xy+8y2−68x+24y−12=017 x ^ { 2 } - 12 x y + 8 y ^ { 2 } - 68 x + 24 y - 12 = 0


A) θ=26.6∘\theta = 26.6 ^ { \circ }
x′24+y′216=1\frac { x ^ { \prime 2 } } { 4 } + \frac { y ^ { \prime 2 } } { 16 } = 1
ellipse
center at (0,0) ( 0,0 )
major axis is y′y ^ { \prime } -axis
vertices at (0,±4) ( 0 , \pm 4 )

B) θ=63.4∘\theta = 63.4 ^ { \circ }
(x′−255) 216+(y′+455) 24=1\frac { \left( x ^ { \prime } - \frac { 2 \sqrt { 5 } } { 5 } \right) ^ { 2 } } { 16 } + \frac { \left( y ^ { \prime } + \frac { 4 \sqrt { 5 } } { 5 } \right) ^ { 2 } } { 4 } = 1
ellipse
center at (255,−455) \left( \frac { 2 \sqrt { 5 } } { 5 } , - \frac { 4 \sqrt { 5 } } { 5 } \right)
major axis is x′x ^ { \prime } -axis
vertices at (4+255,−455) \left( 4 + \frac { 2 \sqrt { 5 } } { 5 } , - \frac { 4 \sqrt { 5 } } { 5 } \right) and (−4+255,−455) \left( - 4 + \frac { 2 \sqrt { 5 } } { 5 } , - \frac { 4 \sqrt { 5 } } { 5 } \right)

C) θ=63.4∘\theta = 63.4 ^ { \circ }
x′2=−16y′x ^ { \prime 2 } = - 16 y ^ { \prime }
parabola
vertex at (0,0) ( 0,0 )
focus at (0,−4) ( 0 , - 4 )

D) θ=63.4∘\theta = 63.4 ^ { \circ }
x′216−y′24=1\frac { x ^ { \prime 2 } } { 16 } - \frac { y ^ { \prime 2 } } { 4 } = 1
hyperbola
center at (0,0) ( 0,0 )
transverse axis is the x′x ^ { \prime } -axis
vertices at (±4,0( \pm 4,0 )

Correct Answer

verifed

verified

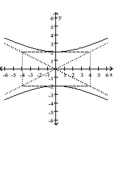
Write an equation for the hyperbola. - Write an equation for the hyperbola. - A) \frac { x ^ { 2 } } { 4 } - \frac { y ^ { 2 } } { 16 } = 1 B) \frac { y ^ { 2 } } { 4 } - \frac { x ^ { 2 } } { 9 } = 1 C) \frac { x ^ { 2 } } { 4 } - \frac { y ^ { 2 } } { 9 } = 1 D) \frac { y ^ { 2 } } { 4 } - \frac { x ^ { 2 } } { 16 } = 1


A) x24−y216=1\frac { x ^ { 2 } } { 4 } - \frac { y ^ { 2 } } { 16 } = 1

B) y24−x29=1\frac { y ^ { 2 } } { 4 } - \frac { x ^ { 2 } } { 9 } = 1

C) x24−y29=1\frac { x ^ { 2 } } { 4 } - \frac { y ^ { 2 } } { 9 } = 1

D) y24−x216=1\frac { y ^ { 2 } } { 4 } - \frac { x ^ { 2 } } { 16 } = 1

Correct Answer

verifed

verified

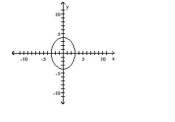
Match the graph to its equation. - Match the graph to its equation. - A) \frac { y ^ { 2 } } { 16 } + \frac { x ^ { 2 } } { 9 } = 1 B) \frac { x ^ { 2 } } { 9 } - \frac { y ^ { 2 } } { 16 } = 1 C) \frac { y ^ { 2 } } { 16 } - \frac { x ^ { 2 } } { 9 } = 1 D) \frac { x ^ { 2 } } { 16 } + \frac { y ^ { 2 } } { 9 } = 1


A) y216+x29=1\frac { y ^ { 2 } } { 16 } + \frac { x ^ { 2 } } { 9 } = 1

B) x29−y216=1\frac { x ^ { 2 } } { 9 } - \frac { y ^ { 2 } } { 16 } = 1

C) y216−x29=1\frac { y ^ { 2 } } { 16 } - \frac { x ^ { 2 } } { 9 } = 1

D) x216+y29=1\frac { x ^ { 2 } } { 16 } + \frac { y ^ { 2 } } { 9 } = 1

Correct Answer

verifed

verified

Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola. - 25y2−16x2=40025 y ^ { 2 } - 16 x ^ { 2 } = 400


A) center at (0,0) ( 0,0 )
transverse axis is xx -axis
vertices: (−5,0) ,(5,0) ( - 5,0 ) , ( 5,0 )
foci: (−41,0) ,(41,0) ( - \sqrt { 41 } , 0 ) , ( \sqrt { 41 } , 0 )
asymptotes of y=−45y = - \frac { 4 } { 5 } and y=45y = \frac { 4 } { 5 }

B) center at (0,0) ( 0,0 )
transverse axis is xx -axis
vertices: (−4,0) ,(4,0) ( - 4,0 ) , ( 4,0 )
foci: (−5,0) ,(5,0) ( - 5,0 ) , ( 5,0 )
asymptotes of y=−45y = - \frac { 4 } { 5 } and y=45y = \frac { 4 } { 5 }

C) center at (0,0) ( 0,0 )
transverse axis is yy -axis
vertices: (0,−4) ,(0,4) ( 0 , - 4 ) , ( 0,4 )
foci: (−41,0) ,(41,0) ( - \sqrt { 41 } , 0 ) , ( \sqrt { 41 } , 0 )
asymptotes of y=−45y = - \frac { 4 } { 5 } and y=45y = \frac { 4 } { 5 }

D) center at (0,0) ( 0,0 )
transverse axis is y-axis
vertices at (0,−4) ( 0 , - 4 ) and (0,4) ( 0,4 )
foci at (0,−41) ( 0 , - \sqrt { 41 } ) and (0,41) ( 0 , \sqrt { 41 } )
asymptotes of y=−45\mathrm { y } = - \frac { 4 } { 5 } and y=45\mathrm { y } = \frac { 4 } { 5 }

Correct Answer

verifed

verified

Find an equation for the parabola described.
-Vertex at (6, 1) ; focus at (6, 3) A) (y−1) 2=−12(x−6) ( y - 1 ) ^ { 2 } = - 12 ( x - 6 )
B) (y−1) 2=12(x−6) ( y - 1 ) ^ { 2 } = 12 ( x - 6 )
C) (x−6) 2=8(y−1) ( x - 6 ) ^ { 2 } = 8 ( y - 1 )
D) (x−6) 2=−8(y−1) ( x - 6 ) ^ { 2 } = - 8 ( y - 1 )

Correct Answer

verifed

verified

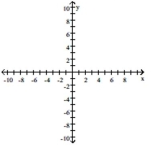
Rotate the axes so that the new equation contains no xy-term. Graph the new equation. - 17x2−12xy+8y2−68x+24y−12=017 x^{2}-12 x y+8 y^{2}-68 x+24 y-12=0 Rotate the axes so that the new equation contains no xy-term. Graph the new equation. - 17 x^{2}-12 x y+8 y^{2}-68 x+24 y-12=0 A) B)


A)
Rotate the axes so that the new equation contains no xy-term. Graph the new equation. - 17 x^{2}-12 x y+8 y^{2}-68 x+24 y-12=0 A) B)

B)
Rotate the axes so that the new equation contains no xy-term. Graph the new equation. - 17 x^{2}-12 x y+8 y^{2}-68 x+24 y-12=0 A) B)

Correct Answer

verifed

verified

Find the vertex, focus, and directrix of the parabola. Graph the equation.
- y2+12y=4x−16y^{2}+12 y=4 x-16
Find the vertex, focus, and directrix of the parabola. Graph the equation. - y^{2}+12 y=4 x-16 A) vertex: ( - 5 , - 6 ) focus: ( - 4 , - 6 ) directrix: x = - 6 B) vertex: ( - 5 , - 6 ) focus: ( - 6 , - 6 ) directrix: x = - 4 C) vertex: ( - 5 , - 6 ) focus: ( - 5 , - 7 ) directrix: y = - 5 D) vertex: ( - 5 , - 6 ) focus: ( - 5 , - 5 ) directrix: y = - 7
A) vertex: (−5,−6) ( - 5 , - 6 )
focus: (−4,−6) ( - 4 , - 6 )
directrix: x=−6x = - 6
Find the vertex, focus, and directrix of the parabola. Graph the equation. - y^{2}+12 y=4 x-16 A) vertex: ( - 5 , - 6 ) focus: ( - 4 , - 6 ) directrix: x = - 6 B) vertex: ( - 5 , - 6 ) focus: ( - 6 , - 6 ) directrix: x = - 4 C) vertex: ( - 5 , - 6 ) focus: ( - 5 , - 7 ) directrix: y = - 5 D) vertex: ( - 5 , - 6 ) focus: ( - 5 , - 5 ) directrix: y = - 7

B) vertex: (−5,−6) ( - 5 , - 6 )
focus: (−6,−6) ( - 6 , - 6 )
directrix: x=−4x = - 4
Find the vertex, focus, and directrix of the parabola. Graph the equation. - y^{2}+12 y=4 x-16 A) vertex: ( - 5 , - 6 ) focus: ( - 4 , - 6 ) directrix: x = - 6 B) vertex: ( - 5 , - 6 ) focus: ( - 6 , - 6 ) directrix: x = - 4 C) vertex: ( - 5 , - 6 ) focus: ( - 5 , - 7 ) directrix: y = - 5 D) vertex: ( - 5 , - 6 ) focus: ( - 5 , - 5 ) directrix: y = - 7


C) vertex: (−5,−6) ( - 5 , - 6 )
focus: (−5,−7) ( - 5 , - 7 )
directrix: y=−5y = - 5
Find the vertex, focus, and directrix of the parabola. Graph the equation. - y^{2}+12 y=4 x-16 A) vertex: ( - 5 , - 6 ) focus: ( - 4 , - 6 ) directrix: x = - 6 B) vertex: ( - 5 , - 6 ) focus: ( - 6 , - 6 ) directrix: x = - 4 C) vertex: ( - 5 , - 6 ) focus: ( - 5 , - 7 ) directrix: y = - 5 D) vertex: ( - 5 , - 6 ) focus: ( - 5 , - 5 ) directrix: y = - 7

D) vertex: (−5,−6) ( - 5 , - 6 )
focus: (−5,−5) ( - 5 , - 5 )
directrix: y=−7y = - 7
Find the vertex, focus, and directrix of the parabola. Graph the equation. - y^{2}+12 y=4 x-16 A) vertex: ( - 5 , - 6 ) focus: ( - 4 , - 6 ) directrix: x = - 6 B) vertex: ( - 5 , - 6 ) focus: ( - 6 , - 6 ) directrix: x = - 4 C) vertex: ( - 5 , - 6 ) focus: ( - 5 , - 7 ) directrix: y = - 5 D) vertex: ( - 5 , - 6 ) focus: ( - 5 , - 5 ) directrix: y = - 7


Correct Answer

verifed

verified

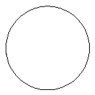
Name the conic. -Name the conic. - A) circle B) parabola C) hyperbola D) ellipse


A) circle
B) parabola
C) hyperbola
D) ellipse

Correct Answer

verifed

verified

Identify the equation without applying a rotation of axes. - 2x2+8xy+16y2−3x−2y+10=02 x ^ { 2 } + 8 x y + 16 y ^ { 2 } - 3 x - 2 y + 10 = 0


A) parabola
B) hyperbola
C) ellipse
D) not a conic

Correct Answer

verifed

verified

Graph the curve whose parametric equations are given.
- x=3cos⁡t,y=2sin⁡t;0≤t≤2πx=3 \cos t, y=2 \sin t ; 0 \leq t \leq 2 \pi

Graph the curve whose parametric equations are given. - x=3 \cos t, y=2 \sin t ; 0 \leq t \leq 2 \pi A) B) C) D)
A)
Graph the curve whose parametric equations are given. - x=3 \cos t, y=2 \sin t ; 0 \leq t \leq 2 \pi A) B) C) D)

B)
Graph the curve whose parametric equations are given. - x=3 \cos t, y=2 \sin t ; 0 \leq t \leq 2 \pi A) B) C) D)

C)
Graph the curve whose parametric equations are given. - x=3 \cos t, y=2 \sin t ; 0 \leq t \leq 2 \pi A) B) C) D)

D)
Graph the curve whose parametric equations are given. - x=3 \cos t, y=2 \sin t ; 0 \leq t \leq 2 \pi A) B) C) D)

Correct Answer

verifed

verified

Find an equation for the hyperbola described. Graph the equation. -Center at (0,0) ;( 0,0 ) ; focus at (13,0) ( \sqrt { 13 } , 0 ) ;vertex at (2,0) ( 2,0 ) Find an equation for the hyperbola described. Graph the equation. -Center at ( 0,0 ) ; focus at ( \sqrt { 13 } , 0 ) ;vertex at ( 2,0 ) A) \frac { y ^ { 2 } } { 4 } - \frac { x ^ { 2 } } { 25 } = 1 B) \frac { x ^ { 2 } } { 4 } - \frac { y ^ { 2 } } { 25 } = 1 C) \frac { y ^ { 2 } } { 25 } - \frac { x ^ { 2 } } { 4 } = 1 D) \frac { x ^ { 2 } } { 25 } - \frac { y ^ { 2 } } { 4 } = 1


A) y24−x225=1\frac { y ^ { 2 } } { 4 } - \frac { x ^ { 2 } } { 25 } = 1
Find an equation for the hyperbola described. Graph the equation. -Center at ( 0,0 ) ; focus at ( \sqrt { 13 } , 0 ) ;vertex at ( 2,0 ) A) \frac { y ^ { 2 } } { 4 } - \frac { x ^ { 2 } } { 25 } = 1 B) \frac { x ^ { 2 } } { 4 } - \frac { y ^ { 2 } } { 25 } = 1 C) \frac { y ^ { 2 } } { 25 } - \frac { x ^ { 2 } } { 4 } = 1 D) \frac { x ^ { 2 } } { 25 } - \frac { y ^ { 2 } } { 4 } = 1

B) x24−y225=1\frac { x ^ { 2 } } { 4 } - \frac { y ^ { 2 } } { 25 } = 1
Find an equation for the hyperbola described. Graph the equation. -Center at ( 0,0 ) ; focus at ( \sqrt { 13 } , 0 ) ;vertex at ( 2,0 ) A) \frac { y ^ { 2 } } { 4 } - \frac { x ^ { 2 } } { 25 } = 1 B) \frac { x ^ { 2 } } { 4 } - \frac { y ^ { 2 } } { 25 } = 1 C) \frac { y ^ { 2 } } { 25 } - \frac { x ^ { 2 } } { 4 } = 1 D) \frac { x ^ { 2 } } { 25 } - \frac { y ^ { 2 } } { 4 } = 1

C) y225−x24=1\frac { y ^ { 2 } } { 25 } - \frac { x ^ { 2 } } { 4 } = 1
Find an equation for the hyperbola described. Graph the equation. -Center at ( 0,0 ) ; focus at ( \sqrt { 13 } , 0 ) ;vertex at ( 2,0 ) A) \frac { y ^ { 2 } } { 4 } - \frac { x ^ { 2 } } { 25 } = 1 B) \frac { x ^ { 2 } } { 4 } - \frac { y ^ { 2 } } { 25 } = 1 C) \frac { y ^ { 2 } } { 25 } - \frac { x ^ { 2 } } { 4 } = 1 D) \frac { x ^ { 2 } } { 25 } - \frac { y ^ { 2 } } { 4 } = 1

D) x225−y24=1\frac { x ^ { 2 } } { 25 } - \frac { y ^ { 2 } } { 4 } = 1
Find an equation for the hyperbola described. Graph the equation. -Center at ( 0,0 ) ; focus at ( \sqrt { 13 } , 0 ) ;vertex at ( 2,0 ) A) \frac { y ^ { 2 } } { 4 } - \frac { x ^ { 2 } } { 25 } = 1 B) \frac { x ^ { 2 } } { 4 } - \frac { y ^ { 2 } } { 25 } = 1 C) \frac { y ^ { 2 } } { 25 } - \frac { x ^ { 2 } } { 4 } = 1 D) \frac { x ^ { 2 } } { 25 } - \frac { y ^ { 2 } } { 4 } = 1

Correct Answer

verifed

verified

Solve the problem. -An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second Tower. The towers are both 12.25 inches tall and stand 70 inches apart. Find the vertical distance from the Roadway to the cable at a point on the road 14 inches from the lowest point of the cable.


A) 2.16 in.
B) 1.76 in.
C) 7.84 in.
D) 1.96 in.

Correct Answer

verifed

verified

Identify the equation without completing the square. - 2x2−4x+y+2=02 x ^ { 2 } - 4 x + y + 2 = 0


A) ellipse
B) hyperbola
C) parabola
D) not a conic

Correct Answer

verifed

verified

Find an equation for the ellipse described. -Center at (0,0) ;( 0,0 ) ; focus at (0,5) ( 0,5 ) ; vertex at (0,−7) ( 0 , - 7 )


A) x224+y249=1\frac { x ^ { 2 } } { 24 } + \frac { y ^ { 2 } } { 49 } = 1

B) x225+y224=1\frac { x ^ { 2 } } { 25 } + \frac { y ^ { 2 } } { 24 } = 1

C) x225+y249=1\frac { x ^ { 2 } } { 25 } + \frac { y ^ { 2 } } { 49 } = 1

D) x249+y224=1\frac { x ^ { 2 } } { 49 } + \frac { y ^ { 2 } } { 24 } = 1

Correct Answer

verifed

verified

Determine the appropriate rotation formulas to use so that the new equation contains no xy-term. - 3x2+5xy+3y2−8x+8y=03 x ^ { 2 } + 5 x y + 3 y ^ { 2 } - 8 x + 8 y = 0


A) x=12x′−32y′x = \frac { 1 } { 2 } x ^ { \prime } - \frac { \sqrt { 3 } } { 2 } y ^ { \prime } and y=32x′+12y′y = \frac { \sqrt { 3 } } { 2 } x ^ { \prime } + \frac { 1 } { 2 } y ^ { \prime }
B) x=2+22x′−2−22y′x = \frac { \sqrt { 2 + \sqrt { 2 } } } { 2 } x ^ { \prime } - \frac { \sqrt { 2 - \sqrt { 2 } } } { 2 } y ^ { \prime } and y=2−22x′+2+22y′y = \frac { \sqrt { 2 - \sqrt { 2 } } } { 2 } x ^ { \prime } + \frac { \sqrt { 2 + \sqrt { 2 } } } { 2 } y ^ { \prime }
C) x=22(x′−y′) x = \frac { \sqrt { 2 } } { 2 } \left( x ^ { \prime } - y ^ { \prime } \right) and y=22(x′+y′) y = \frac { \sqrt { 2 } } { 2 } \left( x ^ { \prime } + y ^ { \prime } \right)
D) x=−y′x = - y ^ { \prime } and y=x′y = x ^ { \prime }

Correct Answer

verifed

verified

Discuss the equation and graph it. - r=32+4sin⁡θr = \frac { 3 } { 2 + 4 \sin \theta } Discuss the equation and graph it. - r = \frac { 3 } { 2 + 4 \sin \theta } A) ellipse, directrix parallel to the polar axis \frac{3}{2} unit below the pole vertices \left(\frac{3}{2}, \frac{\pi}{2}\right) ,\left(\frac{1}{2}, \frac{3 \pi}{2}\right) B) ellipse, directrix perpendicular to the polar axis \frac{3}{2} unit left of the pole vertices \left(\frac{3}{2}, 0\right) ,\left(\frac{1}{2}, \pi\right) C) hyperbola; directrix parallel to the polar axis \frac{3}{4} unit above the pole vertices \left(\frac{1}{2}, \frac{\pi}{2}\right) ,\left(-\frac{3}{2}, \frac{3 \pi}{2}\right) D) hyperbola, directrix perpendicular to the polar axis \frac{3}{4} unit right of the pole vertices \left(\frac{1}{2}, 0\right) ,\left(-\frac{3}{2}, \pi\right)


A) ellipse, directrix parallel to the polar axis 32 \frac{3}{2} unit below the pole vertices (32,π2) ,(12,3π2) \left(\frac{3}{2}, \frac{\pi}{2}\right) ,\left(\frac{1}{2}, \frac{3 \pi}{2}\right)
Discuss the equation and graph it. - r = \frac { 3 } { 2 + 4 \sin \theta } A) ellipse, directrix parallel to the polar axis \frac{3}{2} unit below the pole vertices \left(\frac{3}{2}, \frac{\pi}{2}\right) ,\left(\frac{1}{2}, \frac{3 \pi}{2}\right) B) ellipse, directrix perpendicular to the polar axis \frac{3}{2} unit left of the pole vertices \left(\frac{3}{2}, 0\right) ,\left(\frac{1}{2}, \pi\right) C) hyperbola; directrix parallel to the polar axis \frac{3}{4} unit above the pole vertices \left(\frac{1}{2}, \frac{\pi}{2}\right) ,\left(-\frac{3}{2}, \frac{3 \pi}{2}\right) D) hyperbola, directrix perpendicular to the polar axis \frac{3}{4} unit right of the pole vertices \left(\frac{1}{2}, 0\right) ,\left(-\frac{3}{2}, \pi\right)

B) ellipse, directrix perpendicular to the polar axis 32 \frac{3}{2} unit left of the pole vertices (32,0) ,(12,π) \left(\frac{3}{2}, 0\right) ,\left(\frac{1}{2}, \pi\right)
Discuss the equation and graph it. - r = \frac { 3 } { 2 + 4 \sin \theta } A) ellipse, directrix parallel to the polar axis \frac{3}{2} unit below the pole vertices \left(\frac{3}{2}, \frac{\pi}{2}\right) ,\left(\frac{1}{2}, \frac{3 \pi}{2}\right) B) ellipse, directrix perpendicular to the polar axis \frac{3}{2} unit left of the pole vertices \left(\frac{3}{2}, 0\right) ,\left(\frac{1}{2}, \pi\right) C) hyperbola; directrix parallel to the polar axis \frac{3}{4} unit above the pole vertices \left(\frac{1}{2}, \frac{\pi}{2}\right) ,\left(-\frac{3}{2}, \frac{3 \pi}{2}\right) D) hyperbola, directrix perpendicular to the polar axis \frac{3}{4} unit right of the pole vertices \left(\frac{1}{2}, 0\right) ,\left(-\frac{3}{2}, \pi\right)

C) hyperbola; directrix parallel to the polar axis 34 \frac{3}{4} unit above the pole vertices (12,π2) ,(−32,3π2) \left(\frac{1}{2}, \frac{\pi}{2}\right) ,\left(-\frac{3}{2}, \frac{3 \pi}{2}\right)
Discuss the equation and graph it. - r = \frac { 3 } { 2 + 4 \sin \theta } A) ellipse, directrix parallel to the polar axis \frac{3}{2} unit below the pole vertices \left(\frac{3}{2}, \frac{\pi}{2}\right) ,\left(\frac{1}{2}, \frac{3 \pi}{2}\right) B) ellipse, directrix perpendicular to the polar axis \frac{3}{2} unit left of the pole vertices \left(\frac{3}{2}, 0\right) ,\left(\frac{1}{2}, \pi\right) C) hyperbola; directrix parallel to the polar axis \frac{3}{4} unit above the pole vertices \left(\frac{1}{2}, \frac{\pi}{2}\right) ,\left(-\frac{3}{2}, \frac{3 \pi}{2}\right) D) hyperbola, directrix perpendicular to the polar axis \frac{3}{4} unit right of the pole vertices \left(\frac{1}{2}, 0\right) ,\left(-\frac{3}{2}, \pi\right)

D) hyperbola, directrix perpendicular to the polar axis 34 \frac{3}{4} unit right of the pole vertices (12,0) ,(−32,π) \left(\frac{1}{2}, 0\right) ,\left(-\frac{3}{2}, \pi\right)
Discuss the equation and graph it. - r = \frac { 3 } { 2 + 4 \sin \theta } A) ellipse, directrix parallel to the polar axis \frac{3}{2} unit below the pole vertices \left(\frac{3}{2}, \frac{\pi}{2}\right) ,\left(\frac{1}{2}, \frac{3 \pi}{2}\right) B) ellipse, directrix perpendicular to the polar axis \frac{3}{2} unit left of the pole vertices \left(\frac{3}{2}, 0\right) ,\left(\frac{1}{2}, \pi\right) C) hyperbola; directrix parallel to the polar axis \frac{3}{4} unit above the pole vertices \left(\frac{1}{2}, \frac{\pi}{2}\right) ,\left(-\frac{3}{2}, \frac{3 \pi}{2}\right) D) hyperbola, directrix perpendicular to the polar axis \frac{3}{4} unit right of the pole vertices \left(\frac{1}{2}, 0\right) ,\left(-\frac{3}{2}, \pi\right)

Correct Answer

verifed

verified

Match the equation to the graph. - (y−2) 2=6(x−2) ( y - 2 ) ^ { 2 } = 6 ( x - 2 )


A)
Match the equation to the graph. - ( y - 2 ) ^ { 2 } = 6 ( x - 2 ) A) B) C) D)

B)
Match the equation to the graph. - ( y - 2 ) ^ { 2 } = 6 ( x - 2 ) A) B) C) D)
C)
Match the equation to the graph. - ( y - 2 ) ^ { 2 } = 6 ( x - 2 ) A) B) C) D)

D)
Match the equation to the graph. - ( y - 2 ) ^ { 2 } = 6 ( x - 2 ) A) B) C) D)

Correct Answer

verifed

verified

Solve the problem. -An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second Tower. The towers stand 50 inches apart. At a point between the towers and 15 inches along the road from the Base of one tower, the cable is 1 inches above the roadway. Find the height of the towers.


A) 6.75 in.
B) 5.75 in.
C) 6.25 in.
D) 8.25 in.

Correct Answer

verifed

verified

Showing 41 - 60 of 197

Related Exams

Exam 1

Functions and Their Graphs

301 Questions

Exam 2

Linear and Quadratic Functions

301 Questions

Exam 3

Polynomial and Rational Functions

350 Questions

Exam 4

Exponential and Logarithmic Functions

518 Questions

Exam 5

Trigonometric Functions

366 Questions

Exam 6

Analytic Trigonometry

402 Questions

Exam 7

Applications of Trigonometric Functions

103 Questions

Exam 8

Polar Coordinates; Vectors

270 Questions

Exam 10

Systems of Equations and Inequalities

235 Questions

Exam 11

Sequences; Induction; the Binomial Theorem

238 Questions

Exam 12

Counting and Probability

108 Questions

Exam 13

A Preview of Calculus: the Limit, Derivative, and Integral of a Function

145 Questions

Exam 14

Review

228 Questions

Show Answer