Correct Answer

verified
Correct Answer
verified
Multiple Choice
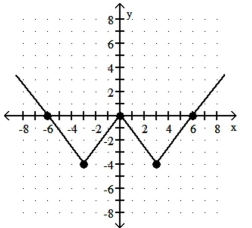
The graph of the function f is shown below. Match the function g with the correct graph.
-
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
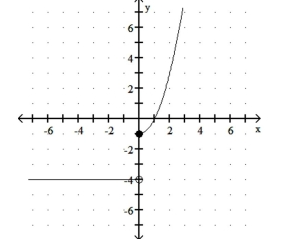
Write an equation for the piecewise function.
-
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Short Answer
Find the requested function value.
-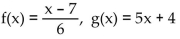 Find
Find 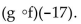 A) -16
B) -36
C) 324
D)
A) -16
B) -36
C) 324
D) 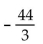
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine algebraically whether the function is even, odd, or neither even nor odd. -
A) Even
B) Odd
C) Neither
Correct Answer

verified
Correct Answer
verified
Multiple Choice
For the pair of functions, find the indicated sum, difference, product, or quotient. -f(x) =5+x, g(x) =4|x| Find (g/f) (x) .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Short Answer
The given point is on the graph of y = f(x). Find a point on the graph of y = g(x). -g(x)=f(x-1) ;(4,14) A) (4,15) B) (3,14) C) (5,14) D) (4,13)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Using the graph, determine any relative maxima or minima of the function and the intervals on which the function is
increasing or decreasing. Round to three decimal places when necessary.
-
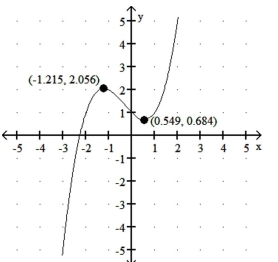
A) relative maximum: 2.056 at x=-1.215 ; relative minima: 0.684 at x=0.549 and 1 at x=0 ; increasing (-1.215,0.549) ; decreasing
B) relative maximum: 0.684 at x=0.549 ; relative minimum: 2.056 at x=-1.215 ; increasing (-1.215,0.549) ; decreasing
C) no relative maxima or minima; increasing decreasing (-1.215,0.549)
D) relative maximum: 2.056 at x=-1.215 ; relative minimum: 0.684 at x=0.549 ; increasing decreasing (-1.215,0.549)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the function. Use the graph to find any relative maxima or minima.
-
A) Relative minimum of -4 at x=1
B) No relative extrema
C) Relative maximum of -4 at x=0
D) Relative minimum of -4 at x=0
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve. -The time T necessary to make an enlargement of a photo negative varies directly as the area A of the enlargement. If 315 seconds are required to make a 5 -by- 7 enlargement, find the time required for a 6 -by- 10 enlargement.
A) 480 sec
B) 660 sec
C) 600 sec
D) 540 sec
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The graph of the function f is shown below. Match the function g with the correct graph.
-g(x) = 2f(x)
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Short Answer
Solve. -At Allied Electronics, production has begun on the X-15 Computer Chip. The total cost function is given by C(x)=7 x+14 and the total profit function is given by where x represents the number of boxes of computer chips produced. The total revenue function, R(x) , is such that R(x)=C(x)+P(x) . Find R(x) . A) B) C) D)
Correct Answer

verified
Correct Answer
verified
Short Answer
For the pair of functions, find the indicated sum, difference, product, or quotient. - Find (fg)(3) A) -53 B) -8 C) -280 D) 56
Correct Answer

verified
Correct Answer
verified
Multiple Choice
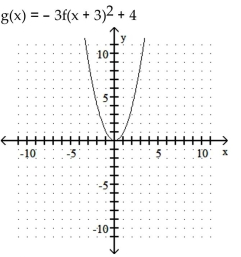
The graph of the function f is shown below. Match the function g with the correct graph.
-
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the domain and range of the function.
-![Determine the domain and range of the function. - A) domain: ( - \infty , - 5 ] range: ( - \infty , 1 ] B) domain: ( - \infty , \infty ) range: ( - \infty , 1 ] C) domain: ( - \infty , \infty ) ; range: ( - \infty , \infty ) D) domain: ( - \infty , - 5 ) \cup ( - 5 , \infty ) range: ( - \infty , 1 ) \cup ( 1 , \infty )](https://d2lvgg3v3hfg70.cloudfront.net/TB34225555/11ec84ca_e272_d75e_a43c_95cdf638afa9_TB34225555_11.jpg)
A) domain: range:
B) domain: range:
C) domain: range:
D) domain: range:
Correct Answer

verified
Correct Answer
verified
Short Answer
Answer the question. -How can the graph of be obtained from the graph of A) Shift it horizontally 1 units to the left. Reflect it across the x -axis. Shift it 6 units up. B) Shift it horizontally 1 units to the right. Reflect it across the x -axis. Shift it 6 units up. C) Shift it horizontally 1 units to the right. Reflect it across the y-axis. Shift it 6 units up. D) Shift it horizontally 1 units to the right. Reflect it across the y-axis. Shift it 6 units down.
Correct Answer

verified
Correct Answer
verified
Short Answer
Find an equation of variation for the given situation. - p varies directly as q , and p=1 when A) B) p=4 q C) p=3 q D) p=2 q
Correct Answer

verified
Correct Answer
verified
Showing 141 - 157 of 157
Related Exams