A) Neither
B) Even
C) Odd
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Perform the requested operation or operations. - Find .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Choose the one alternative that best completes the statement or answers the question.
Graph the piecewise-defined function.
-
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Give the equation of the function g whose graph is described. -The graph of is reflected across the -axis. This graph is then vertically stretched by a factor of . Finally, the graph is shifted 8 units downward.
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Sketch the graph of y1 as a solid line or curve. Then sketch the graph of y2 as a dashed line or curve by one or more of
these: a vertical and/or horizontal shift of the graph y1, a vertical stretch or shrink of the graph of y1, or a reflection of the
graph of y1 across an axis.
-

A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Fill in the blanks to complete the statement.
-The graph of can be obtained by shifting horizontally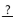 units to the 11ecc462_eee5_8183_841e_b1b874fd7cdc_TB8181_00 , vertically shrinking by a factor of 11ecc462_eee5_8183_841e_b1b874fd7cdc_TB8181_00 and then shifting vertically11ecc462_eee5_8183_841e_b1b874fd7cdc_TB8181_00 units in the11ecc462_eee5_8183_841e_b1b874fd7cdc_TB8181_00 direction.
units to the 11ecc462_eee5_8183_841e_b1b874fd7cdc_TB8181_00 , vertically shrinking by a factor of 11ecc462_eee5_8183_841e_b1b874fd7cdc_TB8181_00 and then shifting vertically11ecc462_eee5_8183_841e_b1b874fd7cdc_TB8181_00 units in the11ecc462_eee5_8183_841e_b1b874fd7cdc_TB8181_00 direction.
A) 9 ; left; ; upward
B) left; ; upward
C) ; right; ; downward
D) 9 ; right; 0.1; 8.5; upward
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the function on your calculator to determine the domain and range from the graph. -
A) Domain: ; range:
B) Domain: ; range:
C) Domain: ; range:
D) Domain: ; range:
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find a direct relationship between x and y. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem.
-The following information pertains to a bakery which makes donuts.
 Make a scatterplot of the data. Based upon the scatterplot, what type of function would best model the data?
Make a scatterplot of the data. Based upon the scatterplot, what type of function would best model the data?
A) Constant function
B) Quadratic function
C) Linear function
D) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the domain of the given function. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the intervals on which the function is increasing, decreasing, and constant.
-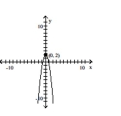
A) Increasing on ; Decreasing on
B) Increasing on ; Decreasing on
C) Increasing on ; Decreasing on
D) Increasing on ; Decreasing on
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Choose the one alternative that best completes the statement or answers the question.
-What symmetry does the graph of exhibit?
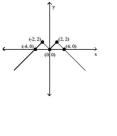
A) origin
B) -axis
C) -axis
D) no symmetry
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the (x,y) pair for the value of the parameter. - and for
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use an equation to solve the problem. -On Monday, an investor bought 100 shares of stock. On Tuesday, the value of the shares went up . How much did the investor pay for the 100 shares if he sold them Wednesday morning for ?
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the range of the function. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the domain of the given function. -
A)
B) All real numbers
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the inverse of the function. -
A)
B)
C) Not a one-to-one function
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the function and determine if it has a point of discontinuity at x = 0. If there is a discontinuity, tell whether it is removable or non-removable. -
A) ![]()
Yes; non-removable
B) ![]()
No
C) ![]()
No
D) ![]()
Yes; removable
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine algebraically whether the function is even, odd, or neither even nor odd. -
A) Even
B) Odd
C) Neither
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the intervals on which the function is increasing, decreasing, and constant.
-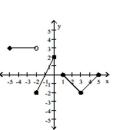
A) Increasing on and ; Decreasing on ; Constant on
B) Increasing on and ; Decreasing on ; Constant on
C) Increasing on and ; Decreasing on and
D) Increasing on ; Decreasing on and ; Constant on
Correct Answer

verified
Correct Answer
verified
Showing 21 - 40 of 362
Related Exams