Filters
Question type
Study Flashcards

 Differentiate the function f(x) =5e3x2\text { Differentiate the function } f ( x ) = 5 e ^ { 3 x ^ { 2 } }


A) 30xe6x30 x e ^ { 6 x }
B) 15xe3x215 x e ^ { 3 x ^ { 2 } }
C) 15e3x215 e ^ { 3 x ^ { 2 } }
D) 30xe3x230 x e ^ { 3 x ^ { 2 } }
E) 15e6x15 e ^ { 6 x }

Correct Answer

verifed

verified

 Find ft(x)  if f(x) =log⁡5(x3−1x3−6) \text { Find } f ^ {t } ( x ) \text { if } f ( x ) = \log _ { 5 } \left( \frac { x ^ { 3 } - 1 } { x ^ { 3 } - 6 } \right)


A) ft(x) =x2−5(x3−1) (x2−6) f ^ { t } ( x ) = \frac { x ^ { 2 } - 5 } { \left( x ^ { 3 } - 1 \right) \left( x ^ { 2 } - 6 \right) }
B) ft(x) =(x3−1) (x3−6) ln⁡(5) f ^ { t } ( x ) = \frac { \left( x ^ { 3 } - 1 \right) } { \left( x ^ { 3 } - 6 \right) \ln ( 5 ) }
C) ft(x) =−15x2(x3−1) (x3−6) f ^ { t } ( x ) = \frac { - 15 x ^ { 2 } } { \left( x ^ { 3 } - 1 \right) \left( x ^ { 3 } - 6 \right) }
D) ft(x) =x3−6(x3−1) ln⁡(5) f ^ { t } ( x ) = \frac { x ^ { 3 } - 6 } { \left( x ^ { 3 } - 1 \right) \ln ( 5 ) }
E) ft(x) =−15x2(x3−1) (x3−6) ln⁡(5) f ^ { t } ( x ) = \frac { - 15 x ^ { 2 } } { \left( x ^ { 3 } - 1 \right) \left( x ^ { 3 } - 6 \right) \ln ( 5 ) }

Correct Answer

verifed

verified

 Find the derivative of the function f(x) =13arcsin⁡(x−1) . \text { Find the derivative of the function } f ( x ) = 13 \arcsin ( x - 1 ) \text {. }


A) 131+2x−x2\frac { 13 } { \sqrt { 1 + 2 x - x ^ { 2 } } }
B) 132x−x2\frac { 13 } { \sqrt { 2 x - x ^ { 2 } } }
C) 131−4x+x2\frac { 13 } { \sqrt { 1 - 4 x + x ^ { 2 } } }
D) 132x+x2\frac { 13 } { \sqrt { 2 x + x ^ { 2 } } }
E) 134x−x2\frac { 13 } { \sqrt { 4 x - x ^ { 2 } } }

Correct Answer

verifed

verified

Identify the graph which has the following characteristics. f(0) =−2ft(x) =2,−∞<x<∞\begin{array} { l } f ( 0 ) = - 2 \\f ^ { t } ( x ) = 2 , - \infty < x < \infty\end{array} Identify the graph which has the following characteristics. \begin{array} { l } f ( 0 ) = - 2 \\ f ^ { t } ( x ) = 2 , - \infty < x < \infty \end{array} A) Graph 2 B) Graph 3 C) Graph 1 D) Graph 4 E) none of the above Identify the graph which has the following characteristics. \begin{array} { l } f ( 0 ) = - 2 \\ f ^ { t } ( x ) = 2 , - \infty < x < \infty \end{array} A) Graph 2 B) Graph 3 C) Graph 1 D) Graph 4 E) none of the above


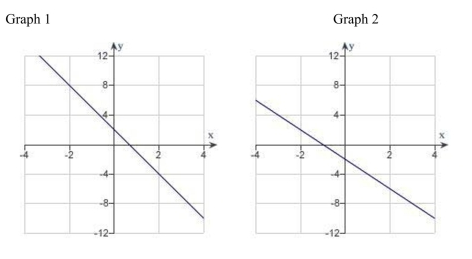
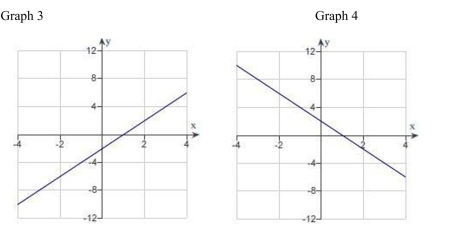
A) Graph 2
B) Graph 3
C) Graph 1
D) Graph 4
E) none of the above

Correct Answer

verifed

verified

Determine all values of , (if any) , at which the graph of the function has a horizontal tangent. y(x) =x4−4x+4y ( x ) = x ^ { 4 } - 4 x + 4


A) x=1x = 1
B) x=0x = 0 and x=−1x = - 1
C) x=0x = 0 and x=1x = 1
D) x=0x = 0
E) The graph has no horizontal tangents.

Correct Answer

verifed

verified

Complete two iterations of Newton's Method for the function using the initial guess . Round all numerical values in your answer to four decimal places.


A)
nxnf(xn) f′(xn) f(xn) f′(xn) xn−f(xn) f′(xn) 11.31.00000.0068−3.60214.902124.90210.2675−0.26750.00684.8953\begin{array}{|c|c|c|c|c|c|}\hline n & x_{n} & f\left(x_{n}\right) & f^{\prime}\left(x_{n}\right) & \frac{f\left(x_{n}\right) }{f^{\prime}\left(x_{n}\right) } & x_{n}-\frac{f\left(x_{n}\right) }{f^{\prime}\left(x_{n}\right) } \\\hline 1 & 1.3 & 1.0000 & 0.0068 & -3.6021 & 4.9021 \\\hline 2 & 4.9021 & 0.2675 & -0.2675 & 0.0068 & 4.8953 \\\hline\end{array}

B)
nxnf(xn) f′(xn) f(xn) f′(xn) xn−f(xn) f′(xn) 11.30.2675−0.9636−0.27761.577621.57760.96360.0068−0.27761.8552\begin{array}{|c|c|c|c|c|c|}\hline n & x_{n} & f\left(x_{n}\right) & f^{\prime}\left(x_{n}\right) & \frac{f\left(x_{n}\right) }{f^{\prime}\left(x_{n}\right) } & x_{n}-\frac{f\left(x_{n}\right) }{f^{\prime}\left(x_{n}\right) } \\\hline 1 & 1.3 & 0.2675 & -0.9636 & -0.2776 & 1.5776 \\\hline 2 & 1.5776 & 0.9636 & 0.0068 & -0.2776 & 1.8552 \\\hline\end{array}

C)
nxnf(xn) f′(xn) f(xn) f′(xn) xn−f(xn) f′(xn) 11.30.9636−0.2675−3.60214.902124.90211.00000.0068146.6399−141.7378\begin{array}{|c|c|c|c|c|c|}\hline n & x_{n} & f\left(x_{n}\right) & f^{\prime}\left(x_{n}\right) & \frac{f\left(x_{n}\right) }{f^{\prime}\left(x_{n}\right) } & x_{n}-\frac{f\left(x_{n}\right) }{f^{\prime}\left(x_{n}\right) } \\\hline 1 & 1.3 & 0.9636 & -0.2675 & -3.6021 & 4.9021 \\\hline 2 & 4.9021 & 1.0000 & 0.0068 & 146.6399 & -141.7378 \\\hline\end{array}

D)
nxnf(xn) f′(xn) f(xn) f′(xn) xn−f(xn) f′(xn) 11.30.2675−0.9636−0.27761.577621.5776−0.0068−1.00000.00681.5708\begin{array}{|c|c|c|c|c|c|}\hline n & x_{n} & f\left(x_{n}\right) & f^{\prime}\left(x_{n}\right) & \frac{f\left(x_{n}\right) }{f^{\prime}\left(x_{n}\right) } & x_{n}-\frac{f\left(x_{n}\right) }{f^{\prime}\left(x_{n}\right) } \\\hline 1 & 1.3 & 0.2675 & -0.9636 & -0.2776 & 1.5776 \\\hline 2 & 1.5776 & -0.0068 & -1.0000 & 0.0068 & 1.5708 \\\hline\end{array}

E)
nxnf(xn) f′(xn) f(xn) f′(xn) xn−f(xn) f′(xn) 11.30.9636−0.96360.00681.293221.29321.0000−1.0000−3.60214.8953\begin{array}{l}\begin{array} { | c | c | c | c | c | c | } \hline n & x _ { n } & f \left( x _ { n } \right) & f ^ { \prime } \left( x _ { n } \right) & \frac { f \left( x _ { n } \right) } { f ^ { \prime } \left( x _ { n } \right) } & x _ { n } - \frac { f \left( x _ { n } \right) } { f ^ { \prime } \left( x _ { n } \right) } \\\hline 1 & 1.3 & 0.9636 & - 0.9636 & 0.0068 & 1.2932 \\\hline 2 & 1.2932 & 1.0000 & - 1.0000 & - 3.6021 & 4.8953 \\\hline\end{array}\end{array}

Correct Answer

verifed

verified

Find the derivative of the function. f(x) =x85−3xf ( x ) = x ^ { 8 } \sqrt { 5 - 3 x }


A) ft(x) =x7(5−51x) 25−3xf ^ { t} ( x ) = \frac { x ^ { 7 } ( 5 - 51 x ) } { 2 \sqrt { 5 - 3 x } }
B) ft(x) =x7(80−3x) 25−3xf ^ { t } ( x ) = \frac { x ^ { 7 } ( 80 - 3 x ) } { 2 \sqrt { 5 - 3 x } }
C) ft(x) =x7(80+51x) 25−3xf ^ { t } ( x ) = \frac { x ^ { 7 } ( 80 + 51 x ) } { 2 \sqrt { 5 - 3 x } }
D) ft(x) =x7(5+3x) 25−3xf ^ { t } ( x ) = \frac { x ^ { 7 } ( 5 + 3 x ) } { 2 \sqrt { 5 - 3 x } }
E) ft(x) =x7(80−51x) 25−3xf ^ { t } ( x ) = \frac { x ^ { 7 } ( 80 - 51 x ) } { 2 \sqrt { 5 - 3 x } }

Correct Answer

verifed

verified

Suppose the position function for a free-falling object on a certain planet is given by s(t) =−14t2+v0t+s0s ( t ) = - 14 t ^ { 2 } + v _ { 0 } t + s _ { 0 } . A silver coin is dropped from the top of a building that is 1370 feet tall. Find velocity of the coin at impact. Round your answer to the three decimal places.


A) −286.705ft/sec- 286.705 \mathrm { ft } / \mathrm { sec }
B) −138.492ft/sec- 138.492 \mathrm { ft } / \mathrm { sec }
C) −111.041ft/sec- 111.041 \mathrm { ft } / \mathrm { sec }
D) −276.984ft/sec- 276.984 \mathrm { ft } / \mathrm { sec }
E) −261.984ft/sec- 261.984 \mathrm { ft } / \mathrm { sec }

Correct Answer

verifed

verified

ladder feet long is leaning against the wall of a house (see figure) . The base of the ladder is pulled away from the wall at a rate of feet per second. Find the rate at which the angle Between the ladder and the wall of the house is changing when the base of the ladder is feet from The wall. Round your answer to three decimal places. ladder feet long is leaning against the wall of a house (see figure) . The base of the ladder is pulled away from the wall at a rate of feet per second. Find the rate at which the angle Between the ladder and the wall of the house is changing when the base of the ladder is feet from The wall. Round your answer to three decimal places. 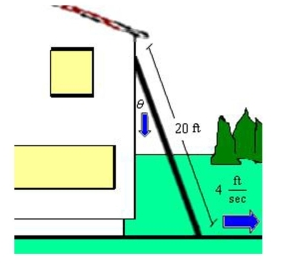A) 0.242 \mathrm { rad } / \mathrm { sec } B) 0.190 \mathrm { rad } / \mathrm { sec } C) 2.168 \mathrm { rad } / \mathrm { sec } D) 3.804 \mathrm { rad } / \mathrm { sec } E) 0.278 \mathrm { rad } / \mathrm { sec }


A) 0.242rad/sec0.242 \mathrm { rad } / \mathrm { sec }
B) 0.190rad/sec0.190 \mathrm { rad } / \mathrm { sec }
C) 2.168rad/sec2.168 \mathrm { rad } / \mathrm { sec }
D) 3.804rad/sec3.804 \mathrm { rad } / \mathrm { sec }
E) 0.278rad/sec0.278 \mathrm { rad } / \mathrm { sec }

Correct Answer

verifed

verified

man 6 feet tall walks at a rate of feet per second away from a light that is 15 feet above the ground (see figure) . When he is feet from the base of the light, at what rate is the Length of his shadow changing? man 6 feet tall walks at a rate of feet per second away from a light that is 15 feet above the ground (see figure) . When he is feet from the base of the light, at what rate is the Length of his shadow changing? 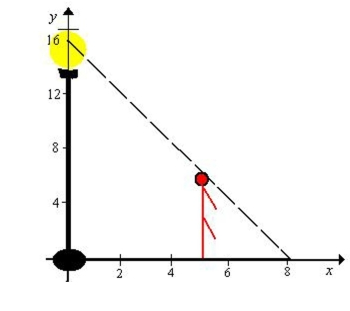A) \frac { 5 } { 2 } \mathrm { ft } / \mathrm { sec } B) \frac { 65 } { 3 } \mathrm { ft } / \mathrm { sec } C) \frac { 26 } { 3 } \mathrm { ft } / \mathrm { sec } D) \frac { 3 } { 65 } \mathrm { ft } / \mathrm { sec } E) \frac { 1 } { 2 } \mathrm { ft } / \mathrm { sec }


A) 52ft/sec\frac { 5 } { 2 } \mathrm { ft } / \mathrm { sec }
B) 653ft/sec\frac { 65 } { 3 } \mathrm { ft } / \mathrm { sec }
C) 263ft/sec\frac { 26 } { 3 } \mathrm { ft } / \mathrm { sec }
D) 365ft/sec\frac { 3 } { 65 } \mathrm { ft } / \mathrm { sec }
E) 12ft/sec\frac { 1 } { 2 } \mathrm { ft } / \mathrm { sec }

Correct Answer

verifed

verified

 Find the derivative of the trigonometric function f(s) =s3tan⁡s. \text { Find the derivative of the trigonometric function } f ( s ) = s ^ { 3 } \tan s \text {. }


A) ft(s) =s3sec⁡2s+3s2tan⁡sf ^ { t } ( s ) = s ^ { 3 } \sec ^ { 2 } s + 3 s ^ { 2 } \tan s
B) ft(s) =s3sec⁡2s+2s2tan⁡sf ^ { t } ( s ) = s ^ { 3 } \sec ^ { 2 } s + 2 s ^ { 2 } \tan s
C) ft(s) =3s2tan⁡s−s2sec⁡2sf ^ {t } ( s ) = 3 s ^ { 2 } \tan s - s ^ { 2 } \sec ^ { 2 } s
D) ft(s) =s2sec⁡2s−3s2tan⁡sf ^ {t } ( s ) = s ^ { 2 } \sec ^ { 2 } s - 3 s ^ { 2 } \tan s
E) ft(s) =s3sec⁡s+3s2tan⁡sf ^ { t } ( s ) = s ^ { 3 } \sec s + 3 s ^ { 2 } \tan s

Correct Answer

verifed

verified

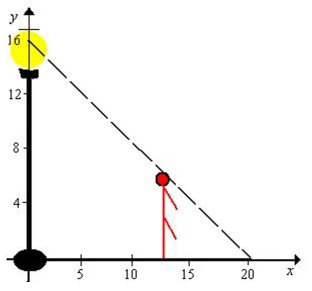
A man 6 feet tall walks at a rate of feet per second away from a light that is 15 feet above the ground (see figure) . When he is feet from the base of the light, at what rate is the Tip of his shadow moving? A man 6 feet tall walks at a rate of feet per second away from a light that is 15 feet above the ground (see figure) . When he is feet from the base of the light, at what rate is the Tip of his shadow moving? A) \frac { 1 } { 2 } \mathrm { ft } / \mathrm { sec } B) 50 \mathrm { ft } / \mathrm { sec } C) \frac { 3 } { 50 } \mathrm { ft } / \mathrm { sec } D) \frac { 9 } { 2 } \mathrm { ft } / \mathrm { sec } E) \frac { 50 } { 3 } \mathrm { ft } / \mathrm { sec }


A) 12ft/sec\frac { 1 } { 2 } \mathrm { ft } / \mathrm { sec }
B) 50ft/sec50 \mathrm { ft } / \mathrm { sec }
C) 350ft/sec\frac { 3 } { 50 } \mathrm { ft } / \mathrm { sec }
D) 92ft/sec\frac { 9 } { 2 } \mathrm { ft } / \mathrm { sec }
E) 503ft/sec\frac { 50 } { 3 } \mathrm { ft } / \mathrm { sec }

Correct Answer

verifed

verified

 Find an equation of the line that is tangent to the graph of the function f(x) =7x\text { Find an equation of the line that is tangent to the graph of the function } f ( x ) = \frac { 7 } { \sqrt { x } } and parallel to the line 7x+2y−18=07 x + 2 y - 18 = 0 .


A) 7x+y+21=07 x + y + 21 = 0
B) 9x+y−18=09 x + y - 18 = 0
C) 9x+2y+9=09 x + 2 y + 9 = 0
D) 7x+2y−21=07 x + 2 y - 21 = 0
E) 7x+2y−14=07 x + 2 y - 14 = 0

Correct Answer

verifed

verified

Find the derivative of the function. f(θ) =75sin⁡22θf ( \theta ) = \frac { 7 } { 5 } \sin ^ { 2 } 2 \theta


A) ft(θ) =−28sin⁡2θcos⁡2θ5f ^ { t } ( \theta ) = - \frac { 28 \sin 2 \theta \cos 2 \theta } { 5 }
B) ft(θ) =28cos⁡2θ5f ^ {t } ( \theta ) = \frac { 28 \cos 2 \theta } { 5 }
C) ft(θ) =28sin⁡2θcos⁡2θ5f ^ { t } ( \theta ) = \frac { 28 \sin 2 \theta \cos 2 \theta } { 5 }
D) ft(θ) =7sin⁡2θcos⁡2θ5f ^ {t } ( \theta ) = \frac { 7 \sin 2 \theta \cos 2 \theta } { 5 }
E) ft(θ) =28sin⁡2θ5f ^ { t } ( \theta ) = \frac { 28 \sin 2 \theta } { 5 }

Correct Answer

verifed

verified

 Find an equation to the tangent line to the graph of the function f(x) =tan⁡8x\text { Find an equation to the tangent line to the graph of the function } f ( x ) = \tan ^ { 8 } x at the point (4π5,0.078) \left( \frac { 4 \pi } { 5 } , 0.078 \right) . The coefficients below are given to two decimal places.


A) y=−1.31x+3.36y = - 1.31 x + 3.36
B) y=1.31x+3.36y = 1.31 x + 3.36
C) y=1.06x+3.36y = 1.06 x + 3.36
D) y=−1.31x−3.36y = - 1.31 x - 3.36
E) y=1.06x−3.36y = 1.06 x - 3.36

Correct Answer

verifed

verified

 Find dydx by implicit differentiation. \text { Find } \frac { d y } { d x } \text { by implicit differentiation. } x3+8x+x13y−y6=4x ^ { 3 } + 8 x + x ^ { 13 } y - y ^ { 6 } = 4


A) dydx=3x2+8+13x12y6y5−x13\frac { d y } { d x } = \frac { 3 x ^ { 2 } + 8 + 13 x ^ { 12 } y } { 6 y ^ { 5 } - x ^ { 13 } }
B) dydx=3x2+8+13y5y5−13x\frac { d y } { d x } = \frac { 3 x ^ { 2 } + 8 + 13 y } { 5 y ^ { 5 } - 13 x }
C) dydx=3x2+8+13x12y5y5−x13\frac { d y } { d x } = \frac { 3 x ^ { 2 } + 8 + 13 x ^ { 12 } y } { 5 y ^ { 5 } - x ^ { 13 } }
D) dydx=3x2+8+x13y6y5−x13\frac { d y } { d x } = \frac { 3 x ^ { 2 } + 8 + x ^ { 13 } y } { 6 y ^ { 5 } - x ^ { 13 } }
E) dydx=3x2−8+13x12y6y5−x13\frac { d y } { d x } = \frac { 3 x ^ { 2 } - 8 + 13 x ^ { 12 } y } { 6 y ^ { 5 } - x ^ { 13 } }

Correct Answer

verifed

verified

The ordering and transportation cost C for the components used in manufacturing a product is C=160(280x2+xx+40) ,x≥1C = 160 \left( \frac { 280 } { x ^ { 2 } } + \frac { x } { x + 40 } \right) , x \geq 1 where CC is measured in thousands of dollars and xx is the order size in hundreds. Find the rate of change of CC with respect to xx for x=24x = 24 . Round your answer to two decimal places.


A) −6.44- 6.44 thousand dollars per hundred
B) 8.048.04 thousand dollars per hundred
C) 3.283.28 thousand dollars per hundred
D) −4.92- 4.92 thousand dollars per hundred
E) −7.96- 7.96 thousand dollars per hundred

Correct Answer

verifed

verified

 Use the quotient rule to differentiate the following function f(s) =2ss5+7 and \text { Use the quotient rule to differentiate the following function } f ( s ) = \frac { 2 s } { s ^ { 5 } + 7 } \text { and } evaluate ft(−2) f ^ { t } ( - 2 )


A) ft(−2) =545f ^ { t } ( - 2 ) = \frac { 54 } { 5 }
B) ft(−2) =−543125f ^ { t } ( - 2 ) = - \frac { 54 } { 3125 }
C) ft(−2) =54125f ^ { t } ( - 2 ) = \frac { 54 } { 125 }
D) ft(−2) =−545f ^ {t } ( - 2 ) = - \frac { 54 } { 5 }
E) ft(−2) =−54125f ^ { t } ( - 2 ) = - \frac { 54 } { 125 }

Correct Answer

verifed

verified

 Find the derivative of the function f(x) =x6ex. \text { Find the derivative of the function } f ( x ) = x ^ { 6 } e ^ { x } \text {. }


A) 6x5+ex6 x ^ { 5 } + e ^ { x }
B) 6x5+xex6 x ^ { 5 } + x e ^ { x }
C) x5ex(x+6) x ^ { 5 } e ^ { x } ( x + 6 )
D) 6x5ex6 x ^ { 5 } e ^ { x }
E) x5exx ^ { 5 } e ^ { x }

Correct Answer

verifed

verified

 Evaluate the derivative of the function f(t) =6t+35t−1 at the point (5,118) . \text { Evaluate the derivative of the function } f ( t ) = \frac { 6 t + 3 } { 5 t - 1 } \text { at the point } \left( 5 , \frac { 11 } { 8 } \right) \text {. }


A) ft(t) =−78f ^ {t } ( t ) = - \frac { 7 } { 8 }
B) ft(t) =7192f ^ { t} ( t ) = \frac { 7 } { 192 }
C) ft(t) =78f ^ { t } ( t ) = \frac { 7 } { 8 }
D) ft(t) =−2126f ^ { t } ( t ) = - \frac { 21 } { 26 }
E) ft(t) =−7192f ^ { t } ( t ) = - \frac { 7 } { 192 }

Correct Answer

verifed

verified

Showing 141 - 160 of 191

Related Exams

Exam 1

Graphs and Models

114 Questions

Exam 2

A Preview of Calculus

92 Questions

Exam 4

Extrema on an Interval

147 Questions

Exam 5

Antiderivatives and Indefinite Integration

167 Questions

Exam 6

Slope Fields and Eulers Method

85 Questions

Exam 7

Area of a Region Between Two Curves

120 Questions

Exam 8

Basic Integration Rules

127 Questions

Exam 9

Sequences

179 Questions

Exam 10

Conics and Calculus

120 Questions

Exam 11

Vectors in the Plane

125 Questions

Exam 12

Vector-Valued Functions

83 Questions

Exam 13

Introduction to Functions of Several Variables

124 Questions

Exam 14

Iterated Integrals and Area in the Plane

118 Questions

Exam 15

Vector Fields

108 Questions

Exam 16

Exact First-Order Equations

45 Questions

Show Answer