FiltersDone

Question type

Essay

Multiple Choice

Short Answer

True False

Matching

Exam 8: Probability Distributions and Statistics

Show Answer

Share

---

All types

Filters

Study FlashcardsPractice ExamLearn

Question 111

Multiple Choice

Review LaterAdd Note

Review Later

Bob, the proprietor of Midland Lumber, feels that the odds in favor of a business deal going through are 7 to 6. What is the (subjective) probability that this deal will not materialize?

A) 0.4647
B) 0.4622
C) 0.4615
D) 0.4460

E) B) and C)
F) All of the above

Correct Answer

verified

Show Answer

Question 112

Multiple Choice

Review LaterAdd Note

Review Later

The daily earnings X of an employee who works on a commission basis are given by the following probability distribution. Find the employee's expected earnings.

A) E(X) = 71.75
B) E(X) = 79.50
C) E(X) = 73.50
D) E(X) = 77.25

E) A) and D)
F) B) and D)

Correct Answer

verified

Show Answer

Question 113

Multiple Choice

Review LaterAdd Note

A survey was conducted of graduates of Harvard College 15 years after graduation. In the survey, the pay of graduates in different fields who had perviously taken off 18 months, often to care for children, was compared with the pay for graduates who had not taken time off. The average financial penalty for those who had taken time off is summarized in the following table: Find the mean of the financial penalty for the graduates who have taken off. What is the standard deviation for these data?

If a sample of 8 batteries is selected from a lot of 11, of which 4 are defective, what is the expected number of defective batteries? Round your answer to next whole number.

Find to four decimal places for the given values of n, x, and p.

Ruth, the owner of a mail-order business, estimates that the probability that a household receiving one of her catalogs will place an order with her is 0.3. How many catalogs must Ruth send out to ensure that the chance of obtaining at least one order is 55% or better? ​

The IQs of students at Wilson Elementary School were measured recently and found to be normally distributed with a mean of 100 and a standard deviation of 15. What the probability that a student selected at random will have IQ of or less?

The manager of a certain toy company has decided to accept a shipment of electronic games if none of a random sample of 20 is found to be defective. What is the probability 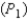that he will accept the shipment if 15% of the electronic games is defective? What is the probability 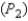that he will accept the shipment if 8% of the electronic games is defective? ​ ​

Let Z be the standard normal variable. Find the value of z if z satisfies P(Z < -z) = 0.8643.

Give the range of values that the random variable X may assume and classify the random variable as finite discrete, infinite discrete, or continuous. ​ X = The number of times a die is thrown until a 5 appears.

Find the value of the probability of the standard normal variable Z corresponding to the shaded area under the standard normal curve. P ( Z < 1.37 )

The general manager of the Service Department of a television company has estimated that the time that elapses between the dates of purchase and the dates on which the 19-inch. sets manufactured by the company first require service is normally distributed with a mean of months and a standard deviation of months. ​ If the company gives a 1-year warranty on parts and labor for these sets, determine the percentage of sets manufactured and sold by the company that may require service before the warranty period runs out. ​

An examination consisting of ten true-or-false questions was taken by a class of 100 students. The probability distribution of the random variable X, where X denotes the number of questions answered correctly by a randomly chosen student, is represented by the accompanying histogram. The rectangle with base centered on the number 8 is missing. What should be the height of this rectangle? ​ ​

Use the appropriate normal distribution to approximate the resulting binomial distribution. ​ A marksman's chance of hitting a target with each of his shots is 60%. If he fires 30 shots, what is the probability of his hitting the target between 12 and 21 times, inclusive? ​

Suppose that one-half of the new buildings in a town are in violation of the building code. If a building inspector inspects seven of the buildings, find the probability 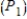that the first five buildings will pass the inspection and the remaining two will fail the inspection. Then find the probability 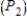that just five of the buildings will pass inspection. ​

Give the range of values that the random variable X may assume and classify the random variable as finite discrete, infinite discrete, or continuous. ​ X = The distance a commuter travels to work ​

An examination consisting of ten true-or-false questions was taken by a class of 100 students. The probability distribution of the random variable X, where X denotes the number of questions answered correctly by a randomly chosen student, is represented by the accompanying histogram. The rectangle with base centered on the number 8 is missing. What should be the height of this rectangle? ​ ​ height = __________

A Christmas tree light has an expected life of 100 hr and a standard deviation of 3 hr. Estimate the probability that one of these Christmas tree lights will last between 94 and 106 hr. __________ Suppose 170,000 of these Christmas tree lights are used by a large city as part of its Christmas decorations. Estimate the number of lights that will require replacement between 70 and 130 hr of use. __________

Cards are selected one at a time without replacement from a well-shuffled deck of 52 cards until a jack is drawn. Let X denote the random variable that gives the number of cards drawn. What values may X assume?

A bank has two automatic tellers at its main office and two at each of its three branches. The number of machines that break down on a given day, along with the corresponding probabilities, are shown in the following table: Find the expected number of machines that will break down on a given day.